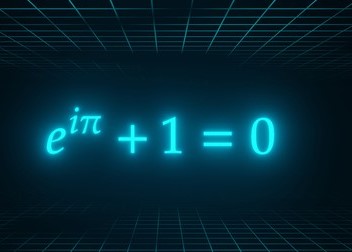
Every day in your life, you come across many many things – like a normal household stuff to a very powerful super computer. Some of the objects you observe are filled with commonplace monotony while some of them clasp your attention because of their charm and beauty. Today, we are going to discuss something “really beautiful” and “complex” stuff, at the same time. This so called “stuff” isn’t any kind of physical identity or abstract entity, but rather a maths equation. An equation, so good, that it was actually honored with the tag ‘The Most Beautiful Equation in Maths’.

 

Euler’s Identity – The Most Beautiful Equation in Maths

Euler’s identity has been named as the most gorgeous equation in mathematics. This identity is an equality which is also compared to a Shakespearean sonnet and described as “the most beautiful equation.” This equation is a distinct instance of a foundational equation in complex arithmetic called Euler’s Formula. Richard Feynman, a physicist, addressed this equivalence in his lectures as “our jewel” and “the most remarkable formula in mathematics.”

 

Euler’s Identity – The Creator

Euler’s identity formation is credited to Swiss mathematician Leonhard Euler. In an interaction with Open University, UK professor Robin Wilson, states Euler as “the most prolific mathematician of all time” and “the Mozart of mathematics”. He also states that “Most of modern mathematics and physics derives from work of Leonhard Euler.’ The professor, in addition for Euler, augments that “many so-called educated people have never heard of him.”. Euler’s equality of identity looks much simpler than of other mathematician like Dirac’s Equation, yet in its ostensible easiness, Leonhard Euler accomplished to arrest some of the greatest elementary principles of mathematics.

 

Euler’s Identity – What does the Equation look like?

Euler’s identity can be written as shown below:

 

Wherein,

is Euler’s number which is considered the base of natural logarithms

is the imaginary unit (known as iota), which by definition satisfies i² = – 1

‘ is pi, the ratio of the circumference of a circle to its diameter

 

It is well-thought-out to be an example of mathematical exquisiteness as it demonstrates a deep connection among the most basic digits in mathematics. This equation is sometimes is directly used in a proof that ‘π’ is transcendental, which suggests the impossibility of squaring the circle.

The equation fuses five of the tremendously significant numbers and digits in arithmetic, which are: –

 

• 1 – the foundation of all other numbers (also a multiplicative identity)

 

• 0 – the notion of nothingness or ‘void’ (also an additive identity)

 

• Pi (π) – the figure that explains a circle (a basic circle constant having value 3.141592…), an irrational numeral

 

• e – the figure that underlies exponential growth, it is also known as ‘Euler’s number’, and has the value of 2.71828, and also befalls extensively in mathematical analysis; another irrational number; it’s also the base of natural logarithms

 

• i – the “imaginary” square root of -1 and a unit of the complex number family

 

Apart from this, these numbers and figures are associated with several practical applications, including communications, navigation, course plotting, energy, engineering, manufacturing, finance, investments, meteorology and climatology, and medicine.

Nevertheless, it is not only comprised of numbers but, Euler’s identity also holds the three most elementary arithmetic operations: addition, multiplication and exponentiation, that gives a structure to maths. There’s undeniably something substantial in its simplicity. It also occurs to be immensely significant to principally every field of math.

 

 

Euler’s Identity – Why Known as “The Most Beautiful Maths Equation”?

Let’s look into why is this equation known as it is known.

 

1. The Entire Euler’s Identity

According to Willian Dunhan, an American mathematician, he states that:

“If you wanna do addition you need 0, if you wanna do multiplication you need 1, if you wanna do calculus you need e, if you wanna do geometry you need π and if you wanna do complex analysis you need i. This is the dream team of numbers and they are all in this one equation.”

 

So, one can infer here that the equation has chiefly, everything.

 

1. 0 and 1

0 is a very special and distinct figure. It marks as the limit or the boundary between the negative and the positive numbers. It is also the solitary number you can’t divide by. Apart from this, it is an additive identity, which means x + 0 = x for all numbers x.

 

For an instance,

Let x = 6

Therefore, 6 + 0 = 6

Likewise with any digit ’x’, an additive identity with 0 gives back the number.

This may appear trivial and insignificant, but in fact, it is a great agreement since it’s an imperative part of what is identified as a group in mathematics – the ‘Group theory’, which is also the maths of symmetry.

Similarly, the number 1 is, indubitably, is a multiplicative identity, which means m x 1 = m, for all numbers m.

 

For an instance,

Let m = 6

Therefore, 6 x 1 = 6

Likewise with any digit ’m’, a multiplicative identity with 1 gives back the number.

 

1. Π or π

The figure ‘π’ appears in maths in all divisions, whether it be number theory or probability or even trigonometry, π is everywhere. Let’s see what is more into π.

To understand π better, we will look into circles. A circle is a figure which is round and without any vertex. It has certain entities within it, like radius, diameter, circumference, area, chord, tangents etc. Circles are associated with both symmetry and periodicity, and these singularities are happening in loads of diverse events in nature and settings in mathematics. Like an exemplar, it ranges from the permeation of heat to arbitrary walks and the vibration of electromagnetic waves, to densities of statistical distributions, and much more.

At the moment if you look at the definition of π, you can generally say that π is the circumference of a circle divided by its diameter. It’s easy till now, right? But you might be wondering, that since it’s the case of ratio, the actual answer might be in terms of fraction of whole numbers. However, what’s fascination in case of π is that even it is demarcated as a ratio, it cannot be written as a fraction of whole numbers. To make it simpler, we can call π, an irrational entity which is in fact transcendental and never – ending. A celebrity of arithmetic for certain.

1. e

The figure ‘e’ in maths is another aspect. It’s a little trying to define it. Well, e is generally a number founded and discovered by Euler himself. It too, like π, is an irrational number and never-ending. At the time Euler discovered it, he had a certain calculation mechanism which was something like:

 

 

Subsequently, the notion was compressed and e was given a value of 2.7182818.

If you look at ‘e’ in terms of higher mathematical entity, like in calculus, then you will see that there is an identity for the differential operator (shown below).

If we differentiate the above function, we will get the property;

This property is noteworthy, as it helps to solve differential equation and other calculus problems. Since nearly all of the physical laws and systems can be defined by differential equations, these are substantially important in physics, biology, mathematics, and science in general.

 

Another manner, in which you can define e, is the “base of the exponential function with the property that the rate of change at a given moment is equal to its value at that moment.”

 

1. i

The figure ‘i’ in maths is another feature allied with complex number. The study of i and the functions used by it is known as complex analysis. In order to understand what i is, we can say that it is a numeral which has the following property –

You might be wondering now, that there doesn’t exist any negative numbers, then how do you explain i. Well, mathematically, if you tend to multiply any two negative numbers, then you’ll get a positive number as their product. Thus, i is nevertheless, an imaginary unit.

 

Complex numbers can be represented as:

 

Wherein, a and b are real numbers.

Likewise, complex analysis is the study of such complex numbers, variables and functions.

Apart from this, these numbers are used in radar technology, differential equations and also in quantum mechanics.

Overall Equation – Numerical Operations and Geometric Transformations

 

Herein, we will discuss only the geometrical way of looking into Euler’s identity (We won’t be discussing the proof).

 

We will first look into what is known as ‘translation’.  In simple worlds, translation is a sort of movement in equal distances in same direction. For instance, if you think of it in maths, let’s add the digit 4 to every number on the number line.

You will now look into a pattern like this;

-1 + 4 = 3

0 + 4 = 4

1 + 4 = 5

And so on…

Nevertheless, you will now notice that the entire number line shifts by 4. This transformation is what we call as translation.

Easy, right?

 

Note here that, for zero, there won’t be any kind of translation, because anything added to 0 is the number itself.

 

Now, let’s look into the same translation with a different viewpoint. We were adding positive number to the numbers on the number line. But what if we add a negative number to the numbers on the number line.

Herein, the pattern generated would be somewhat like this:

-1 + (-4) = – 5

0 + (-4) = – 4

1 + (-4) = – 3

And so on…

 

You can also see it, as subtracting. Here also translation is taking place, but what is different is that the translation takes place in the opposite direction, and this is what we call as ‘inverse translation’. This also happens to change the positing of number on the number line, by the specified digits.

 

Let’s look into the case of multiplication. If you multiple every number on the number line by 2, you will get:

2 x 2 = 4

2 x 3 = 6

2 x 4 = 8

And so on…

Therefore, the numbers are getting stretched on the number line.

If we see the same in case of division, we will get:

2 / 2 = 1

2 / 3 = 2 / 3

2 / 4 = 1 / 2

And so on…

Herein, there is an inverse transformation taking place again, as dividing 2 by 2 is same as multiplying 2 by ½.

Keep these concepts in mind.

Look, if you reflect any number two times, like (-1) (-1), you will get back to 1.

 

The second concept that we will look into what is known as ‘rotation’. In order to understand it, you need to look into a graphical format. Let’s say I gave a point (0,1) which is the number 1 in y – axis or the numbers 0 and 1 in the xy plane. If I ask you to turn this point in a clockwise manner by 90 degrees, you’ll obtain another such point, which would be (1,0). Herein, you have 1 in the x – axis. Such phenomena of rotating digits in the plane are what we call as ‘rotation’.

Another term here is the degree measurement. We have something called as ‘radians’, who is also a friend to degree, yet it looks somewhat different than degree, but do the same task. We won’t be discussing this much, but understand that;

 

180 degrees corresponds to π radians, and similarly, 2 π would be equal to 360 degrees.

Clear till here, right?

Let’s apply what we have learnt into Euler’s identity.

Here, the left-hand part, say that the rotation is by π radians and the right-hand part say that the reflection is by number zero. Therefore, what Euler’s identity is saying is that:

 

“A rotation of 180 degrees is the same as a reflection through 0.”

 

 

By Ayachi Mishra

 

 

 

 

 References:

https://www.cantorsparadise.com/the-most-beautiful-equation-in-the-world-5ab6e49c363

https://en.wikipedia.org/wiki/Euler%27s_identity

http://www.bbc.com/earth/story/20160120-the-most-beautiful-equation-is-eulers-identity

https://www.businessinsider.com/most-beautiful-math-science-equations-2016-3?IR=T